The Trick That Makes Understanding Physics as Simple as Drawing a Picture: Physics Help Room

One of the most powerful tools in physics is also one of the simplest—as simple as drawing a picture. The idea is just to sketch the potential energy curve of a system, and imagine that it's a hill that a particle is sliding along. Then the behavior of the particle on the hill will be qualitatively very similar to the actual motion of a particle subject to that potential.

I'll show you how to apply this idea to a few examples, including how you can understand at a glance the elliptical shape of the orbit of a planet like Earth around a star like the Sun. Physicists use these ideas all over the place, from classical mechanics to quantum mechanics and quantum field theory and string theory. So let's dive in.

You've hopefully learned a bit about potential energy before, like the gravitational potential $U = m g y$ of a projectile. Say you throw a particle of mass $m$ straight up in the air. Ignoring things like air resistance, once the particle leaves your hand the only force that's acting on it will be gravity $mg$ pulling straight down:

$$F = -mg.$$

The minus sign here means that the force is pointing downward. Then the $F = ma$ equation for the $y$ coordinate that measures the height of the particle above the ground is

$$-mg = ma \implies a = -g.$$

The vertical acceleration is a constant, $g$, pointing back toward the ground.

It follows that the total energy $E = K + U$ of the particle is a constant throughout its flight:

$$E = \frac{1}{2} m v^2 +mgy = \mathrm{constant}.$$

That's easy to check if you know a little calculus; just take the derivative of $E$ with respect to time. The things that depend on time here are $v(t)$ and $y(t)$. The derivative of $v^2$ is $2 v a$, where the acceleration $a$ is the derivative of $v$, and the derivative of $y$ is just the velocity $v$ again. So we find

$$\frac{\mathrm{d}E}{\mathrm{d}t} = m v a + m g v = m v(a + g).$$

But $a = -g$, and so $a + g=0$! So the total energy is indeed a constant.

The potential energy $U = mgy$ is just a straight line with slope $mg$:

Imagine that this line were a frictionless hill, and you set a particle down on top of it. What would happen? The particle would of course just slide right down. Likewise, if you held a ball up in the air at some height and then let it go, it would obviously fall down to the ground. In other words, the behavior of the actual projectile is very similar to the behavior of an imaginary particle that we release from the same $y$ coordinate on the "potential hill."

The steeper the hill is, the more force there will be pulling the particle down. So we expect that the force on the particle is proportional to the slope of the hill. And the fact that the particle is pulled down the hill rather than pushed up means that the force will actually go like minus the slope. This is precisely the relation between force and potential energy:

$$\mathrm{Force} = - \mathrm{Slope(Potential)}.$$

In other words, $F(y)$ is minus the derivative of $U(y)$ with respect to $y$:

$$F(y) = - \frac{\mathrm{d}}{\mathrm{d}y}U(y).$$

We can see that explicitly for our projectile: the slope of $U=mgy$ is $mg$, and so the force is minus that, just as expected.

The fact that the motion of the falling projectile mirrors the motion of a particle sliding down the potential hill might not seem all that helpful in this simple example, where it's easy enough to just solve the $F = ma$ equation and determine $y(t)$. But in even slightly more complicated systems, the $F = ma$ equation might be very hard—if not impossible—to solve in closed form. Then being able to predict what the motion will look like just by sketching a picture of the potential becomes very helpful.

I'll show you two progressively more complicated examples. The first is just a simple pendulum, which from the name you might think is simple enough, but its $F = ma$ equation is actually pretty complicated. And the second example is the shape of the orbit of the Earth around the Sun.

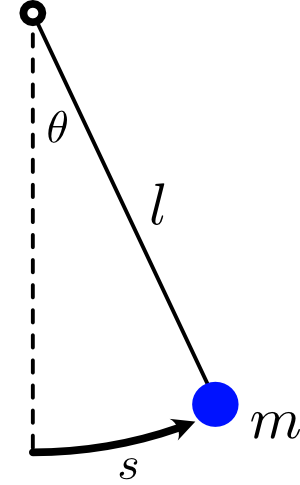
So here's a simple pendulum. It's just a particle of mass $m$ attached to a massless rod of length $l$, which is pivoted at the other end. I made a video all about pendulums if you want to learn more of the details about them. There I explain how to show that the $F = ma$ equation for the angle $\theta$ that the pendulum makes with the vertical is

$$a_\theta = - \frac{g}{l} \sin\theta,$$

where $a_\theta$ is the acceleration of $\theta$.

You might remember learning that the solution for a pendulum is very simple: it's just a sine or cosine as a function of time! But that's only true when the angle $\theta$ is small, meaning that the pendulum is close to its equilibrium position at $\theta = 0.$ In that special case we can apply the "small-angle approximation", which is the fact that $\sin \theta \approx \theta$ for tiny $\theta$'s. But outside of that case, we have to deal with the $\sin\theta$ term that shows up on the right-hand-side of this equation, and that makes it pretty complicated. It doesn't have a simple solution in terms of things like sines and cosines.

We can see what the motion looks like in general by numerically solving the $F= ma$ equation on a computer, like in the animation below:

You can drag the sliders here to set the initial angle and angular speed of the pendulum, and then press start to watch what happens. For example, set the initial angle slider to some relatively small value and then press start. You can see that it indeed oscillates back and forth like a cosine function. But now drag the initial angle slider all the way to the right. Press reset and then press start again. Now it doesn't look like a cosine anymore—the curve is much flatter at the peaks and the valleys. In other words, the pendulum spends a long time turning around at its maximum angles. It gradually slows down and then gradually picks up speed again as it falls—much more slowly than it turned around when the angle was small.

Can we explain this behavior if we don't know the solution for $\theta(t)$, and we don't have a computer simulation handy?

Let's write down the potential energy again. Set the origin at the pivot point. Then the $y$ coordinate of the particle is $y = -l \cos \theta$, and so the potential energy is

$$U = - m g l \cos \theta.$$

The total energy is the kinetic plus the potential. The speed of the particle is $v = \omega l$, where $\omega$ is the angular speed—i.e. the the rate of change of $\theta(t)$. This is just the familiar formula $v = \omega r$ for a particle moving around in a circle, where $r = l$ here is the radius. Then the kinetic energy is $K = \frac{1}{2} m v^2 = \frac{1}{2} m l^2 \omega^2$, and the total energy is

$$E = \frac{1}{2} m l^2 \omega^2 - mg l \cos\theta.$$

You can again check that $E$ is a constant by taking its time derivative and applying the $F = ma$ equation.

Here's what the potential looks like:

Once again, the trick is to forget about the pendulum for a moment, and pretend that this is a literal hill, and that we've got a particle sliding along it. Say we set the particle down at some initial position $\theta_0$ and then let it go. What will the motion look like?