Everything You Need To Know About Pendulums: Physics Help Room

Pendulums are really fascinating systems for learning about a lot of physical principles. They can come in all kinds of shapes and sizes, but I'm going to focus on the simple pendulum, which means that we have a ball of mass $m$ attached to a rod of length $l$, which is pivoted at its other end so that the pendulum is free to rotate around. We'll treat the ball as a point particle, and we'll assume that the rod is much lighter than the ball, so that we can effectively treat it as being massless.

We want to learn how to predict the motion of the pendulum. So say if you were to pull it up to some initial angle and then let it go, or if you were to give the ball a kick to set it moving, what's the resulting motion going to look like?

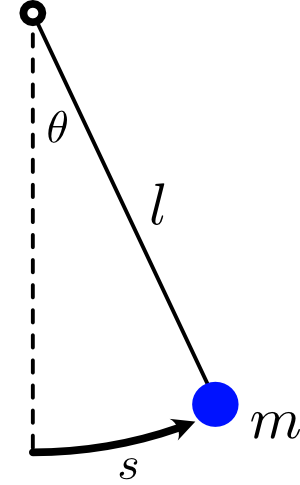
The first thing we should do is to set up some coordinates that specify the position of the pendulum. We can make different choices here, but I think the simplest coordinates to use would either be the angle $\theta$ that the rod makes with the vertical, or the arc length coordinate $s$ that's traced out along the circle that the particle is stuck on. Either one will do the job, and the relation between them is the definition of an angle in radians—it's the arc length divided by the radius:

$$\theta = \frac{s}{l}.$$

Note that $\theta = s = 0$ is the equilibrium position of the pendulum, where it will happily sit at rest at the very bottom.

The basic procedure for predicting motion that we learn about in our first physics class is

1. Draw the free-body diagram that shows all of the forces $\vec{{}F}$ acting on a mass
2. Add up all the forces $\sum \vec{{}F}$, and write down Newton's 2nd law: $\sum \vec{{}F} = m \vec{{}a}$
3. Solve $\sum \vec{{}F} = m \vec{{}a}$ for the trajectory $\vec{{}r}(t)$

That's what we'll do step-by-step for the pendulum. First, the free-body-diagram:

There are only two forces acting on the particle. We've got gravity $mg$ pulling straight down, and we've got the tension $T$ in the rod pulling back toward the center of the circle.

Step two is to add up all the forces and write $\sum \vec{{}F} = m \vec{{}a}$. This is a vector equation, but because the particle is stuck moving around on a circle, we really only care about the component of the force and acceleration that point along the circle:

The tension points radially inward toward the center of the circle, which is perpendicular to the tangent direction that we're actually interested in. So the tension doesn't contribute anything to the tangent direction. The only thing that actually contributes is the component of gravity that points along the circle.

We need to do a tiny bit of geometry to figure out what this force is:

First of all, we can see from the pair of opposite angles that the angle that the tension arrow makes with the vertical is also $\theta$. Then since the tension makes a right angle with the tangent direction, the gravity arrow makes an angle $\frac{\pi}{2} - \theta$ with the tangent. So we have a little right triangle with the gravity arrow making the hypotenuse, one leg pointing tangent to the circle and the other leg pointing perpendicular to the circle. The tangent component is what we're after: it's $mg \sin \theta$ pointing back toward $\theta = 0.$

In practice, there's a faster way to figure out the tangent force. We know it's going to be either $mg \sin \theta$ or $mg \cos \theta$, but how do we pick the right one without going through all this geometry work? The trick is to think about limiting cases. For example, when $\theta = 0$—so that the pendulum is all the way at the bottom of its arc—the tangent direction to the circle is horizontal, and gravity is of course still pointing straight down. So gravity is perpendicular to the tangent direction, and the component of gravity along the circle is zero. That rules out $mg \cos \theta$, since that would have given us $mg \cos(0) = mg$ when $\theta = 0$. It's $mg \sin \theta$ that correctly vanishes when $\theta = 0.$

Now we can write down the component of $\sum \vec{{}F} = m \vec{{}a}$ along the circle. We have the one force $-mg \sin \theta$ (minus because it points back toward equilibrium) and the acceleration $\ddot{s}$:

$$m \ddot{s} = - mg \sin \theta.$$

I'm using dots here to denote rates of change with respect to time. So if $s(t)$ is the position as a function of time, then

$$v = \dot s = \frac{\mathrm{d}{s}}{\mathrm{d}t}$$

is the velocity (the first derivative of $s(t)$), and

$$a = \ddot s = \frac{\mathrm{d}^2{s}}{\mathrm{d}t^2}$$

is the acceleration (the second derivative).

Let's write everything in terms of $\theta$ by remembering that $s = l \theta$. $l$ is a constant, so this equation also implies $\dot s = l \dot \theta$ and $\ddot{s} = l \ddot {\theta}$. Then we get

$$ml \ddot{\theta} = - mg \sin \theta.$$

Finally, we can simplify this to

$$\ddot{\theta} = - \frac{g}{l} \sin \theta.$$

That was step two of Newton's procedure. Step three is to solve this equation for $\theta(t)$. That's actually pretty hard to do. The factor of $\sin \theta$ on the right-hand-side makes this a complicated equation—too complicated for us to be able to write down a simple solution, in general.

But there's one special case where we can write down a simple solution, and that's when $\theta$ is small, meaning that the pendulum never gets very far away from equilibrium. This would be the case if you pulled the pendulum up to some small initial angle and then let it go, or if you only gave it a gentle tap to set it oscillating slightly back and forth. In this special case, we can apply what's known as the small angle approximation. This is the fact that $\sin \theta$ and $\theta$ very closely approximate each other when $\theta$ is small:

$$\sin \theta \approx \theta \quad\quad \theta \ll 1.$$

The easiest way to see this is just to plot $\sin \theta$ and $\theta$ on the same graph:

In general the two curves look nothing like each other. But near the origin, where $|\theta| < 0.5$ radians or so, they're right on top of each other. If you're familiar with Taylor series, $\sin \theta = \theta + \cdots$ is just the first term in the expansion of $\sin \theta$ around $\theta = 0$.

Then provided the pendulum never gets very far away from equilibrium, we can approximate the $F = m a$ equation as

$$\ddot \theta =-\frac{g}{l} \theta.$$

It's going to be convenient to define $\Omega = \sqrt{g/l}$, so that the factor in front of $\theta$ is $-\Omega^2$:

$$\ddot \theta = - \Omega^2 \theta.$$

This is a much simpler equation. We just have to ask ourselves what kind of function $\theta(t)$, when I take its second derivative, gives me back the same function times a negative number. The answer is a sine or cosine!

Recall that the derivative of $\sin$ is $\cos$, and the derivative of $\cos$ is $-\sin$. Then notice that

$$\frac{\mathrm{d}}{\mathrm{d}t} \sin(\Omega t) = \Omega \cos(\Omega t)$$

and

$$\frac{\mathrm{d}}{\mathrm{d}t} \cos(\Omega t) = -\Omega \sin(\Omega t).$$

The factors of $\Omega$ on the right come from the chain rule: the derivative of $\sin(\Omega t)$ with respect to its argument is $\cos(\Omega t)$, and then we multiply by the derivative of $\Omega t$ with respect to $t$, which contributes a factor of $\Omega$.

Alternatively, this factor had to be there by considering the units. $g$ has units of $\mathrm{meters/second^2}$ and $l$ is in $\mathrm{meters}$, so that $\Omega = \sqrt{g/l}$ has units of $1/\mathrm{seconds}.$ $\sin(\Omega t)$ and $\cos(\Omega t)$ are both unitless—the $\mathrm{d}/\mathrm{d}t$ on the left makes those units $1/\mathrm{seconds}$, and we likewise get $\mathrm{1/seconds}$ on the right thanks to the factors of $\Omega$.

Now taking the second derivative, we get

$$\frac{\mathrm{d}^2}{\mathrm{d}t^2} \sin(\Omega t) = -\Omega^2 \sin(\Omega t)$$

and

$$\frac{\mathrm{d}^2}{\mathrm{d}t^2} \cos(\Omega t) = -\Omega^2 \cos(\Omega t),$$

which is exactly what we wanted: the second derivative is $-\Omega^2$ times the function that we started with.

So, the general solution to our $F = ma$ equation when $\theta$ is small is

$$\theta(t) = A \cos (\Omega t) + B \sin(\Omega t).$$

$A$ and $B$ here are two constants that depend on the initial conditions: where was the pendulum and how fast was it moving at $t = 0$? If we plug in $t = 0$ we get

$$\theta(0) = A,$$

so that $A$ corresponds to the initial angle $\theta_0$ of the pendulum. $B$, meanwhile, is related to the initial angular velocity:

$$\dot \theta (t) = -\Omega A \sin(\Omega t) + \Omega B \cos(\Omega t) \implies \dot \theta(0) = \Omega B.$$

So we could alternatively write the general solution as

$$\theta(t) = \theta_0 \cos (\Omega t) + \frac{\dot \theta_0}{\Omega} \sin (\Omega t).$$

There we have it! We've solved for the trajectory of the pendulum given whatever the initial conditions $\theta_0$ and $\dot \theta_0$ are, provided that we don't stray too far away from equilibrium. For example, if we release the pendulum from rest from a small initial angle $\theta_0$, the motion is given by

$$\theta(t) = \theta_0 \cos(\Omega t),$$

where again $\Omega$ was defined as the square root of $g/l$.

There's a lot of interesting physics to notice here. What we've found is that the pendulum oscillates back-and-forth around equilibrium in a sinusoidal pattern. That certainly sounds reasonable—if you pull a pendulum up to a starting angle and let it go, it will oscillate back-and-forth between that angle and the same angle on the opposite side (ignoring things like air resistance and friction from the pivot point). In other words, the motion is periodic.

The speed of the oscillations is characterized by $\Omega$, which is called the natural frequency of the pendulum. The bigger $\Omega$ is, the faster the oscillations will be. Notice that it only depends on the strength of gravity $g$ and the length of the pendulum $l$: the longer the pendulum, the slower the oscillations, and the stronger gravity is, the faster the oscillations. But it doesn't depend on the mass $m$ of the particle. Two pendulums, identical except that one has mass $m$ and the other mass $2m$, will oscillate at the same rate. This is reminiscent of the fact that the acceleration of a falling projectile is always $g$, regardless of its mass.

The time it takes the pendulum to complete one full oscillation is called the period $T$ (not to be confused with the tension). $\cos$ and $\sin$ complete a full oscillation when their arguments increase by $2\pi$. So for example

$$\cos (\Omega t) = \cos(\Omega t + 2\pi).$$

We can alternatively write the right-hand-side as $\cos(\Omega (t + \frac{2\pi}{\Omega}))$. So the pendulum comes back to its starting configuration after time

$$T = \frac{2\pi}{\Omega} = 2\pi \sqrt{\frac{l}{g}}$$

has elapsed.

We again could have guessed this by thinking about the units: the only way to get something with units of $\mathrm{seconds}$ out of $l, g,$ and $m$ is the combination $\sqrt{l/g}$. The period couldn't depend on $m$ because there's nothing to cancel out that factor of $\mathrm{kilograms}.$ That doesn't tell us anything about additional unitless factors that multiply $\sqrt{l/g}$, though, like the $2\pi$ that actually came out in the answer. But thinking about units in physics often gets us 90% of the way there with very little effort!

Also notice that the period doesn't depend on the initial angle $\theta_0$: if we pull two identical pendulums up to initial angles $\theta_0$ and $2\theta_0$, they'll swing back to where they started at the same time, as long as $\theta_0$ is small. That didn't have to be the case—$\theta_0$ is unitless, so we could have multiplied $\sqrt{l/g}$ by any function of $\theta_0$ without changing the units. And in fact at larger angles, the period does depend on the initial angle, as you'll discover if you complete the problem sheet linked at the top of the page.

Here's an animation that plots $\theta(t)$ for initial conditions of your choosing:

You can drag the sliders to set the initial angle and angular speed, and then press start to watch what happens. Notice that when you release the pendulum from rest close to equilibrium, the oscillation indeed looks sinusoidal. But when you release it from a big angle it doesn't. The motion is still periodic—meaning that it repeats itself over and over again—it's just not as simple as a cosine; the peaks and troughs of the graph are much flatter.

On the other hand, if you kick the pendulum very hard by giving it a big initial speed, it doesn't oscillate back-and-forth at all—it swings all the way around the pivot!