We can expand any potential $U(x)$ in powers of $x$ around a stable equilibrium point using a Taylor series, like you might have learned about in your math classes. First, let’s slide our origin over so that it’s on top of whatever equilibrium point we're interested in—that will make the formula simpler:

$$ U(x) = U(0) + U'(0) x + \frac{1}{2!} U''(0) x^2 + \frac{1}{3!}U'''(0) x^3+\cdots. $$

Here’s what’s going on in this formula. First of all, if you’re sitting right at $x = 0$, then when you evaluate the potential you’re obviously going to get $U(0).$ If you take a tiny step away from there, so that $x$ is a small but non-zero number, the potential is still going to be close to $U(0)$, but now it will be shifted slightly away by the slope $U'(0)$ times $x$. Then

$$ U(x) \approx U(0) + U'(0)x $$

is a very good approximation to our function near $x = 0.$ We use this approximation all the time in physics. But it’s actually not that useful to us in this particular case, because remember that we’ve put our origin at a stable equilibrium point, where $U(0) = 0$ and $U'(0) = 0$. To get a better approximation, we have to include the terms with higher powers of $x$ in the Taylor series. By including more and more of these terms, we get a better and better approximation to our function, as you can see by dragging the slider below. And when we add up all the infinite number of terms, we reproduce the exact function!

But we don’t need an infinite number of terms to get a good approximation to our potential near the stable equilibrium point. We just need the first non-zero one—the quadratic term:

$$ U(x) \approx \frac{1}{2} U''(0) x^2. $$

That’s the potential energy of a spring, with spring constant $k = U''(0)$! Then almost any potential energy function, however complicated, reduces to the simple harmonic oscillator potential in the neighborhood of its stable equilibrium points. (The “almost” exception is for the rare case when $U''(0)$ also happens to vanish, in which case we need to include the next term in the series to get a better approximation.)

And this is why the simple harmonic oscillator is so prevalent. Systems tend to settle into stable equilibrium, and small disturbances make them oscillate around it. So the first thing we should do with any potential energy function is find its stable equilibrium points, and then ask what happens when we perturb slightly away from them. A particle that’s released there will oscillate around the equilibrium in simple harmonic motion, with natural frequency

$$ \Omega = \sqrt{\frac{U''(0)}{m}}. $$

To understand the physics farther away from the equilibrium points is usually much harder. The bigger $x$ gets, the more important the higher power corrections in the Taylor series like $x^3$ and $x^4$ become. But we can often get approximate solutions by treating them as perturbations of our harmonic oscillator solution.

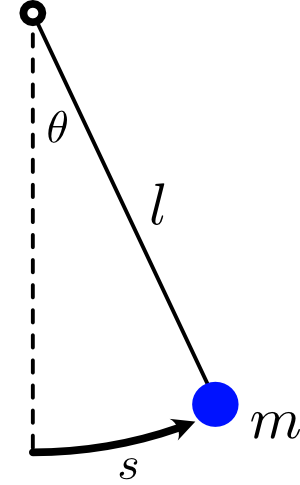
You’ve seen all this in action before if you’ve studied the simple pendulum, though you may or may not have seen it presented in this language. If a pendulum is inclined at an angle $\theta = s/l$, where $s$ is the arc length coordinate that the particle has traced out, then the mass will be at a height $h =l - l \cos (\frac{s}{l})$ above the bottom. (I’ll write the coordinate as $s$ instead of $x$ so we don’t get it confused with the $xy$ coordinates of the point.) Then the potential energy function $U = m g h$ is

$$ U(s) = mg l\left(1 - \cos \left(\frac{s}{l}\right)\right). $$

The stable equilibrium is of course at $s = 0$, where the pendulum hangs straight down at rest. And we can check by taking the derivative:

$$ U'(s) = mg \sin \left(\frac{s}{l}\right) \implies U'(0) = 0. $$

The second derivative is meanwhile

$$ U''(s) = \frac{m g}{ l} \cos \left(\frac{s}{l} \right) \implies U''(0) = \frac{m g}{l}. $$

Note that it’s positive—that’s how we know we’re at a stable equilibrium, as opposed to the top of the arc, where the slope of the potential also vanishes but the second derivative is negative. That’s an unstable equilibrium because if you take a tiny step away from it the pendulum will swing far away.

Our Taylor expansion around equilibrium is then

$$ U(s) \approx \frac{1}{2} \frac{m g}{l} s^2, $$

describing a simple harmonic oscillator with natural frequency

$$ \Omega = \sqrt{\frac{g}{l}}, $$

which is the familiar frequency of a pendulum! Taylor expanding around the equilibrium in this context is often called the small angle approximation, because it amounts to expanding the $F = ma$ equation for the pendulum around $\theta = 0$. In that neighborhood, the system reduces to a simple harmonic oscillator, and so the pendulum sinusoidally oscillates around its equilibrium position.