Dimensional Analysis: Your Physics Superpower!

It's an old quip that Richard Feynman's approach to solving physics problems was a three step procedure:

1. Write down the problem
2. Think very hard
3. Write down the answer

That strategy is all well and good if you're Feynman, but what about for the rest of us?

Well, I can't give you a single trick that will let you write down the solution to any physics problem in the world without any work, but as a matter of fact there is a strategy that can get you most of the way to the answer for many kinds of problems.

It's called dimensional analysis, and it's one of the most essential tools in every physicist's problem-solving toolkit. I'm going to show you how to apply it to three very different problems: finding the oscillation period of a simple pendulum, the binding energy of a hydrogen atom, and the event horizon radius of a black hole.

If you're a beginning physics student, you might already be familiar with the solution of the pendulum problem. But I'm certainly not going to assume that you have experience with the quantum mechanics of the hydrogen atom or the black hole spacetimes of general relativity. And that's the beauty and power of this technique: dimensional analysis is universal, and it's usually step zero in trying to solve any physics problem.

The numbers that we measure in science typically have dimensions—for example, time, length, mass, charge, and so on. And we set up systems of units in order to establish standards for how to compare them: seconds, meters, kilograms, and Coulombs, for example, are the standard "SI" units that we use to measure the aforementioned quantities.

In a given physics problem, we have some list of parameters at our disposal—masses, lengths, charges, and so on, as well as fundamental constants like $c$, $G$, and $\hbar$. And we're looking for an answer with some particular dimensions, like time or energy or whatever. The idea of dimensional analysis is just to figure how we can combine the given input parameters in order to get the correct units of the desired output. Just thinking about how we can assemble the parameters of a problem to get the units right often gets us 90% of the way to the answer to our question with next to no effort!

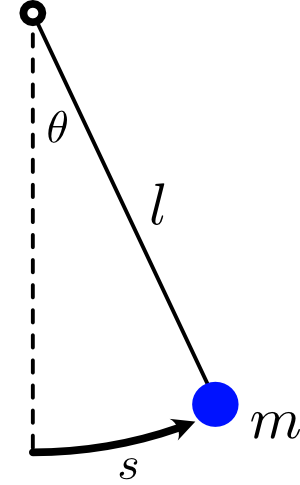
Let's start off with the simple pendulum example. It's a particle of mass $m$ attached to a lightweight rod of length $l$ which is pivoted at its other end. If we pull the pendulum up to some initial angle $\theta_0$ and then let it go, it will oscillate back and forth. The question is, how long does it take to complete a full oscillation? This quantity is called the period $T$ of the pendulum.

If you've learned some mechanics, you might have solved this problem before using $F = ma$. But say you didn't know anything about Newton's laws or differential equations or anything like that, and you only knew about Galileo's experimental observation that falling bodies near the surface of the Earth all experience the same constant downward acceleration $g \approx 10~\mathrm{m/s^2}.$ What could you say then about the period of the pendulum?

The period has units of $\mathrm{seconds}$, and the parameters we have at our disposal are $m$ (in $\mathrm{kilograms}$), $l$ (in $\mathrm{meters}$), $g$ (in $\mathrm{m/s^2}$), and $\theta_0$ (which is unitless). We want to figure out how we can combine these quantities to get something with units of $\mathrm{seconds}$.

The only place that $\mathrm{seconds}$ show up here are in the units of $g$. If we flip $g$ over and take the square-root, we'll get units of

$$\sqrt{\frac{1}{g}} \sim \mathrm{\frac{s}{\sqrt{m}}}.$$

Now we need to get rid of that factor of $\sqrt{\mathrm{m}}$ in the denominator, so we should multiply this by $\sqrt{l}$:

$$T \propto \sqrt{\frac{l}{g}}.$$

That gets us $\mathrm{seconds}$, and so the period of the pendulum must be proportional to this quantity!

With next to no work, dimensional analysis has gotten us the most important part of the answer. In your intro mechanics class, you might have computed that the period is more precisely given by

$$T = 2\pi \sqrt{\frac{l}{g}},$$

with a factor of $2\pi$ sitting in front. Dimensional analysis can't tell us anything about that factor though. $2\pi$ is just a pure number without any units. Thinking about the dimensions alone tells us that the answer has to be proportional to $\sqrt{l/g}$, but it doesn't say anything about whether there's a $2$ or $\pi$ or $\sqrt{17}$ that multiplies it.

Still, the units tell us a lot with minimal effort, like the fact that the oscillations of the pendulum get slower and slower the longer you make the rod. And moreover that the period cannot depend on the mass of the particle: $m$ can't appear in this formula because we don't have another parameter handy with which to cancel out those units of $\mathrm{kg}$. Two pendulums, one with mass $1~\mathrm{kg}$ and the other with mass $2 ~\mathrm{kg}$ will oscillate at the same rate. (There is arguably another mass to play with here—the mass of the Earth. That's actually hiding inside $g$!)

Finally, what happened to the parameter corresponding to the initial angle $\theta_0$? That parameter is unitless, so just like the factors of $2$ and $\pi$, the dimensions alone don't tell us how the period will depend on the initial angle: we could insert any function $f(\theta_0)$ in the answer and still get the correct units,

$$T = 2\pi f(\theta_0) \sqrt{\frac{l}{g}}.$$

As it turns out, $f(\theta_0)\approx 1$ for small initial angles, $\theta_0 \lesssim 0.5$: the period of a pendulum released from a small initial angle doesn't depend on that angle. But at larger angles the period does depend on $\theta_0.$ If the initial angle is very close to $\pi$, for example, so that you release the pendulum from just slightly to the right of pointing straight upward, it takes a long time slowly speeding up from rest before it finally falls. Again, dimensional analysis can't tell us about that aspect of the physics. I explained an alternative way to understand it in this video.

But okay, maybe you thought that example was a little too easy. Let's look at another: the binding energy of a hydrogen atom. This is the amount of energy you would need to kick the electron out of its "orbit" around the proton and send it flying away. This is a quantum mechanics question, but even without knowing any quantum mechanics we can still get most of the answer just by thinking about the units.

So what parameters do we have to play with this time? Classically, the electron experiences a Coulomb force due to the electric field of the proton,

$$F = k\frac{e^2}{r^2}.$$

$k$ here is Coulomb's constant, which evidently has units of

$$k \sim \mathrm{\frac{N \cdot m^2}{C^2}}$$

in order to get $\mathrm{Newtons}$ on both sides of the equation. $e$ is the magnitude of the electric charge of the proton and electron, which are the same up to a sign.

So, we have $k$ and $e$ to work with, as well as the masses of the electron and proton. But the proton is so much heavier than the electron (by a factor of about 2000), that we'll treat the proton as if it's infinitely massive and fixed in place. We make the same approximation when we treat the orbit of a planet around a much more massive star. Then we add the mass $m$ of the electron to our list.

Finally, since this is a quantum mechanics problem, we also have Planck's constant $\hbar$, which sets the scale of quantum effects, and has units of $\mathrm{energy\cdot time}$.

$$m \sim \mathrm{kg},\quad e \sim \mathrm{C},\quad k \sim \mathrm{\frac{N\cdot m^2}{C^2}},\quad \hbar \sim \mathrm{kg\cdot \frac{m^2}{s}}.$$

We want to combine these to get units of energy. The first thing to notice is that we need to cancel out the units of Coulombs, so that $k$ and $e$ have to enter in the combination $k e^2$. Then let's try writing down an answer of the form

$$(ke^2)^a m^b \hbar^c.$$

Its units are

$$\left(\mathrm{\frac{kg \cdot m^3}{s^2}}\right)^a (\mathrm{kg})^b \left( \mathrm{\frac{kg \cdot m^2}{s}} \right)^c.$$

Simplifying, that's

$$\frac{\mathrm{kg}^{a+b+c} \mathrm{m}^{3a+2c}}{\mathrm{s}^{2a+c}}.$$

We want to get energy here, which is measured in $\mathrm{kg\cdot m^2/s^2}$. Therefore, we must have

$$\begin{align} &a+b+c = 1\notag\\ & 3a+2c = 2 \notag\\ & 2a+c = 2 \notag. \end{align}$$

This is a simple system of linear equations—the second pair tells us that $a = 2$ and $c = -2$, and then the first gives $b = 1.$

Thus, dimensional analysis has told us that the binding energy of the hydrogen atom must be proportional to

$$E \propto \frac{m(ke^2)^2}{\hbar^2}.$$

Plugging in the numbers, this gives about $4.36\times 10^{-18}~\mathrm{Joules}$. The experimental result is meanwhile about $2.18 \times 10^{-18}~\mathrm{J}$, so it seems our formula comes with a factor of $1/2$:

$$E =\frac{m(ke^2)^2}{2\hbar^2}.$$

As always, dimensional analysis can't tell us anything about unitless factors like this $2$. But it again got us 90% of the way to the answer, while needing to know next to nothing about quantum mechanics! Now go lookup the solution to the Schrödinger equation for the hydrogen atom in a quantum mechanics textbook for the exact derivation, and you'll appreciate just how efficient dimensional analysis is.

In addition to approximating the proton as infinitely massive compared to the electron, we were also working here in the non-relativistic approximation, meaning that we ignored the speed of light $c$ in our list of parameters. Once we include $c$, we can in fact form a unitless combination of our parameters called the fine structure constant:

$$\alpha = \frac{k e^2}{\hbar c}\approx \frac{1}{137}.$$

Then dimensional analysis can't tell us how $\alpha$ enters into our result for the binding energy, just like it didn't tell us anything about how the pendulum period depends on the unitless initial angle $\theta_0$. Including the effects of special relativity and the quantum mechanical spins of the electron and proton give rise to very small—but calculable, measurable, and very interesting!—corrections to our formula for the binding energy above.

Let's quickly look at one more example, this time from Einstein's theory of gravity. If a massive object like a dying star is compacted into a dense enough ball, it can form a black hole—an object so dense that not even a ray of light can escape its gravitational pull if it gets too close.

How dense would the star have to be? The parameters we have this time are the mass $M$ of the star, the gravitational constant $G$, and the speed of light $c$, with units

$$M \sim \mathrm{kg},\quad G \sim \mathrm{\frac{m^3}{kg\cdot s^2}},\quad c \sim \mathrm{\frac{m}{s}}.$$

We want to find the radius that we would need to squeeze the mass into to form a black hole, so we're looking for units of $\mathrm{meters}.$ First we need to multiply $M$ and $G$ together to cancel out the $\mathrm{kg}$. That gives us $\mathrm{m^3/s^2}$, and so if we further divide by $c^2$ we'll get units of meters:

$$R_H \propto \frac{GM}{c^2}.$$

Again there's a factor of $2$ that we can't get from dimensional analysis (isn't there always...),

$$R_H = \frac{2GM}{c^2}.$$

This is the event horizon radius of a Schwarzschild black hole. If a mass $M$ is compacted into a ball smaller than this radius it will form a black hole. Then if a deep space explorer—or a passing ray of light—is unfortunate enough to approach the black hole, once they cross the horizon radius they can never escape back out. It is the point of no return, from whose bourn no traveler returns.

I haven't proven that to you of course—that would require the full treatment of Einstein's theory of gravity. But we've learned that if such a critical radius exists, it has to take this form proportional to $GM/c^2$.

Whenever you come up against a physics problem in the future, remember to pause before you start diving into complicated equations, and just ask yourself how you can combine the quantities in front of you to get something with the correct units that you're looking for. And when you do solve all your equations to try to find the precise answer, remember check that it does indeed have the correct units. If it doesn't, then you made a mistake somewhere along the line in your derivation, and you know you need to go back and check your work, like I explained in this earlier video.